• Heapsort

• NOTE: Your Device may work slower on a large Dataset!

• • # of Data

  • Sync
  • Randomize
  • Sort

Complexity Analysis

Time Complexity: O(n log n)

Space Complexity: O(1)

How it works

Heap sort is based exclusively upon a binary heap data structure, where we find the largest element and sort it to the end of our unsorted collection. We use the properties of a complete binary tree to sort our collection efficiently.

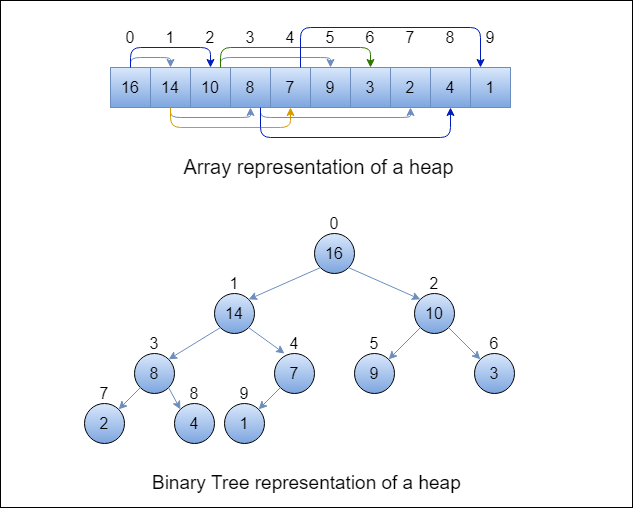
Source: https://miro.medium.com/v2/resize:fit:1266/1*IJDDOZOsFGLpf445qo1XKw.png

Pseudocode Implementation

Heapify(A as array, n as int, i as int) {
    max = i
    leftchild = 2i + 1
    rightchild = 2i + 2
    if (leftchild <= n) and (A[i] < A[leftchild])
        max = leftchild
    else 
        max = i
    if (rightchild <= n) and (A[max] > A[rightchild])
        max = rightchild
    if (max != i)
        swap(A[i], A[max])
        Heapify(A, n, max)
}

// Initialize n as Length of Array
Heapsort(A as array, n as int) {
    for i = n/2 downto 1
        Heapify(A, n ,i)
    
    for i = n downto 2
        exchange A[1] with A[i]
        A.heapsize = A.heapsize - 1
        Heapify(A, i, 0)
}

Source: https://fullyunderstood.com/pseudocodes/heap-sort/

Source: https://en.wikipedia.org/wiki/Heapsort